Our main line of research focus on inference and calibration of financial models such as diffusions and jump-diffusions. We also work with simulation of stochastic processes especially stochastic differential equations and Lévy processes which are important building blocks for models in mathematical finance. We also work with approximation of prices and hedging portfolios for financial derivatives.

Applications of Extreme Values analysis include: modeling of insurance claims using copulas; consequences of higher capital requirements in Basel III recommendations for financial institutes; modeling operational risk related to requirements in Basel III recommendations.

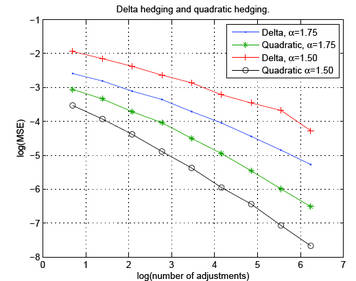
Figure:  Convergence of the discretization error to zero for a digital option in the CGMY model quadratic hedging vs. delta hedging.

In one project we developed an on-line pricing that calculates option prices and their “Greeks” for various models such as Black-Scholes, Merton, Heston, Bates,NIG and NIGCIR.

Publications

<iframe src="https://lup.lub.lu.se/search/organization/3440A41F-05DA-4170-A2EF-41F0323FEC00?embed=1&style=apa" width="100%" height="400" allowtransparency="true" frameborder="0"> </iframe>